概要
軸受定数と摩擦係数
ストライベック曲線(シュトリベック線図・Stribeck curve)は、ドイツ人研究者のRichard Stribeck(リヒャルド・シュトリベック)が20世紀はじめに、すべり軸受の摩擦特性や、転がり軸受の静的負荷能力の実験から、導き出した軸受定数Gに対する摩擦係数の挙動を示す特性曲線です。(図1)
軸受定数Gは単位を持たない無次元数で、ZN/P または、ηN/P として表されます。ここでZ またはη(いーた)は粘度(cSt)、Nは回転数(min-1)、P(Pa)は荷重です。
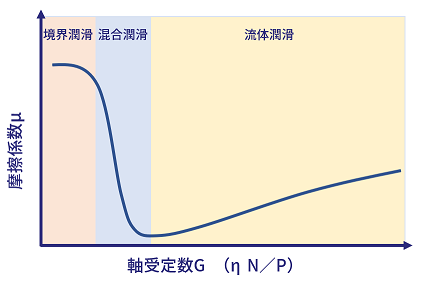
境界潤滑・混合潤滑・流体潤滑
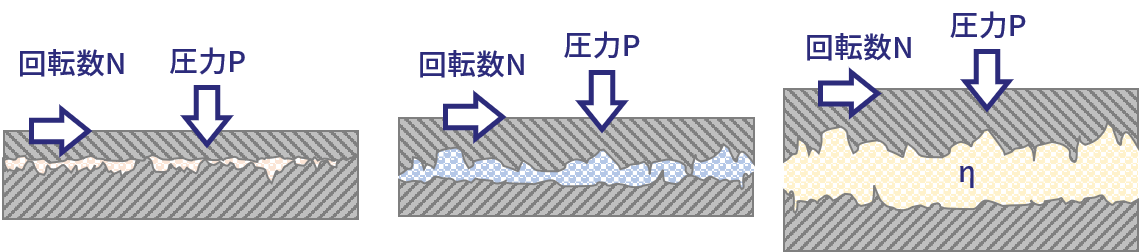
図2 境界潤滑・混合潤滑・流体潤滑
| 境界潤滑 Boundary Lubrication |
混合潤滑 Mixed Lubrication |
流体潤滑 Hydrodynamic Lubrication |
|---|---|---|
物理的・化学的に油膜ではなく吸着膜が荷重を支えている状態です。 |
流体潤滑と混合潤滑が共存している状態です。 |
固体の2面間において液体或いは気体が多く介在し膜内の流体圧力が荷重を支えている状態です。 |
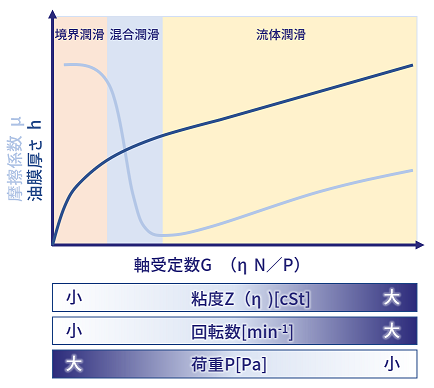
軸受定数と油膜厚さ
ストライベック曲線の上へ便宜的に、潤滑油膜厚さも関係を重ねたグラフが図3です。
一般的に図3のように回転数Nと粘度Z(またはη)が大きいと油膜厚さhも大きくなり、荷重Pが大きいほど油膜厚さhは小さくなります。一般に、静止中や低速回転時には、軌道輪と転動体が油膜形成なく接触しています。
- 粘度Z(η)が大きいと、油膜は厚くなり、
- 回転数Nが大きいと、油膜は厚くなり、
- 荷重Pが小さいと、油膜は厚くなります。
最後に
ストライベック曲線は、物体二面間における摩擦係数の振る舞いを示す曲線として、トライボロジーの世界で非常に多く適用されていますが、実際に実験を行うと、潤滑剤の油性向上剤や極圧添加剤など、様々な影響から、完全にこの通りになるというものではなく、あくまでも概念的な曲線です。
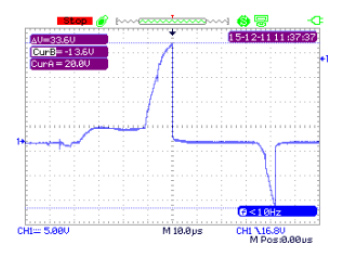
油膜厚さと軸電圧の関係
近年では軸受電流による潤滑劣化や電食の可能性を調べるために、軸電圧の測定が行われますが、それと密接な関係を持つのがこの油膜厚さであり、それが静電容量(キャパシタンス)として捉えられ、油膜厚さの大きさに伴い、オームの法則で軸電圧にも影響を及ぼすことが確認されています。